Universal Order
"Time is what clocks measure"
If the only unit we need to care about when measuring the universe is time, then in a certin sense, our model is nothing other than a very sophisticated clock.
Clocks can be used to provide the invaluable service of describing order. In a literal, physical sense, what this means for our model of the universe is that we have a notion of before and after, and causality to link the two together.
There are however, several kinds of order. We might draw our eyes towards:
- Strong order, in which before/after relationships are defined for all pairs of events, and
- Weak order, in which before/after relationships are defined for only some [1] pairs of events.
[1]Note that ordering obeys transitivity. If A comes before B, and B comes before C, that implies that A comes before C, for all A, B, and C.
In our day-to-day lives, we generally assume, and act as though the universe were strongly-ordered. The main reason we can get away with this is because our day-to-day lives are roughly within 1/15th of a second [2], so discrepancies in ordering usually manifest themselves as a barely-perceptible amount of lag.
[2]
Q:
Where'd this number come from?
A:
Your day-to-day life is probably constrained to Earth. Light takes 130ms to go half-way around the planet, meaning that the far side of the Earth is 1/15th of a second away from you (remember: distance is just time).
Q:
How does this manifest itself as lag?
A:
Because strong ordering is extremely useful, most world-wide computer networks are built to support it. This involves extremely sophisticated systems for synchronizing clocks across the globe [2-1], as well as message-passing back and forth to double-check strong ordering in electronic transactions.
[2-1]Some of them use atomic clocks too, since time is defined w.r.t. a physical atomic process.
However, the underlying physical reality is not strongly ordered, but weakly. At the cost of an amount of time proportional to the distance over which strong ordering is imposed, strong order can be simulated on top of weak ordering [3].
[3]Note that weak ordering can be trivially simulated on top of strong ordering. It's not called 'strong' for nothing.
To see how the physical universe is weakly ordered, consider four events A, B, C, and B, pictured below. We're going to be using quantum electrodynamics (QED), so the events pictured here are electrons either emitting or absorbing photons.
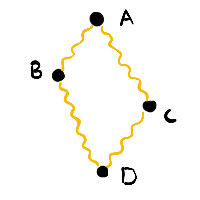
A photon's journey between two events represents a before-after relationship in time. This means that time is ordered w.r.t. A-B, A-C, B-D, and C-D, at the minimum. The question is: is B-C also defined? Since there's no photon traveling between these events, that value is not defined in our perfect universal model, and so time must be weak [4].
[4]You may not find this to be a satisfactory proof. As mentioned before, we simulate strong ordering on top of weak ordering. In the context of our example, this means that we calculate a time between B and C that matches our intuition. For example, you might subtract A-B from A-C, or subtract C-D from B-D.
The problem this approach encounters is that time A-C - A-B may not be equal the time B-D - C-D, which means our calculation may not be deterministic. Why not? While the speed of light is a constant, photons can travel faster or slower than that speed. QED is wild like that.
But how weak? A careful reader may have noticed that because B-C was undefined since there was no photon connecting them, time is defined solely between events that share a connection. Most events at a subatomic scale only have a few connections, and there are a lot of subatomic particles in our universe. This means that our perfect universal model's order is weak to the point of almost non-existence.
Maybe a better word would be 'sparse'. We can formalize our model as an N-dimensional square [5] matrix, where every row or column represents a particle, and the value in a cell is the time the photon [6] took to connect them.

[5]Note that the matrix is symmetric, because photons don't have a direction anyways. Though they may measure time between other events, they are massless, and therefore do not experience time themselves. You'll notice I drew the diagram without arrows on the photons.
[6]
Q:
What about the other elementary particles?
A:
Truly, I am not enough of a particle physicist to tell you. The general idea, of modeling the universe as the sum of its interactions (between fermions and bosons), remains. The main wrench would be the question of gravity, which has so far refused to be folded into the standard model.
To exand this model to all particles, the 'edges' in the sparse matrix would be bosons, and the nodes, their interactions with fermions.
| A | B | C | D | |
| A | A-B | A-C | ||
| B | A-B | B-D | ||
| C | A-C | C-D | ||
| D | B-D | C-D |
The matrix that represents our prefect universal model (and therefore, our universe) would be almost entirely undefined. Which, from a computational perspective, makes it a ripe target for compression.