The Shape of the Universe
Once we've gotten comfortable with the idea of representing the universe as a sparse matrix of particle interactions, we can discard the idea that it's inherently three-dimensional. The matrix itself has an arbitrarily high number of dimensions, and it just so happens that three is a useful answer to the compression puzzle.
What compression puzzle? If we wanted to go back to treating the universe as though it had spatial coordinates, one way would be to treat each cell in the matrix as a constraint (of the form "X and Y are T seconds away from each other"), and the 'shape' of the universe is any mapping of particles onto a lower-numbered field of spatial dimensions that meets all the constraints.
The appearance of the physical universe having three dimensions is the product of the observation that assuming three dimensions allows for the most cohesive solution to the problem. It's not perfect, though. Recognizing that space is non-Euclidean, that space-time (as the field-like solution to this problem is ordinarily called) is curved, is an acknowledgement that our assumption is observed to be false at large distances and high momenta.
The next best approximation (or refinement, if you will), includesinflation. Inflation is observed in that the universe is slightlyhyperbolic, that it exhibits a negative curvature, or that parallel lines tend to get further apart from each other as they move away from the singularity that marks the universe's beginning.
In a time-based perspective, this is equivalent to saying that for three particles X, Y, and Z (all located at great times from each other), the time from X to Z may exceed the time from X to Y plus from Y to Z [1].
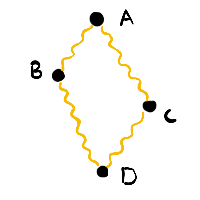
[1]To revisit the example we used for (see also universal order), this proves that A-B plus B-D may not equal A-C plus C-D.

For a physical example of this, consider events X, Y, and Z where X and Y occur very close to the Big Bang before inflation, and Z occurs roughly where you are reading this. The time from X to Y is very small (because the universe is very small before inflation), however the time from X to Z and Y to Z may differ by a large margin, because inflation pushed X and Y a universe apart from each other.
Another interesting observation that falls out of treating the universe as a sparse matrix is the possibility of pocket dimensions [2].
[2]A pocket dimension is a subgraph of the sparse matrix whose intersection with the larger matrix is limited to only a (comparatively) small 'pocket' of interactions. If the intersection is small enough, it won't meaningfully distort the space-time 'solution' of the larger matrix, meaning that the 'solution' of the contents of the pocket can take a different shape. For example you could have a 5D pocket attached to some corner of the 3D universe. Similarly, the size of a pocket may have no relationship with the size of the sub-matrix it connects through; the pocket could be tiny, or vast [2-1].
[2-1]
Q:
How would you detect such a pocket dimension?
A:
Pretty much by definition, you con only detect the pockets that you "reach into", where the interactions that you are aware of bridge the pocket connecting the two universes.